什么是稀疏矩阵?
在科学计算中,经常面临大量的线性稀疏矩阵方程组求解。所谓稀疏矩阵,即元素大部分是0的矩阵(有些资料定义非零元素不超过5%的矩阵,为稀疏矩阵,如下图所示为稀疏矩阵和稠密矩阵的示意图), 矩阵的稀疏性可以用一个分数来量化,即矩阵中零元素的个数除以矩阵中元素的总数。
为何要压缩?
显然,对稀疏矩阵中的非零项进行存储对计算机内存是极大的浪费,因为这些非零项的信息对求解毫无意义,因此在实际操作中往往采用矩阵存储压缩技术。
常见的稀疏矩阵存储压缩格式
(1) Coordinate(COO)/三元组
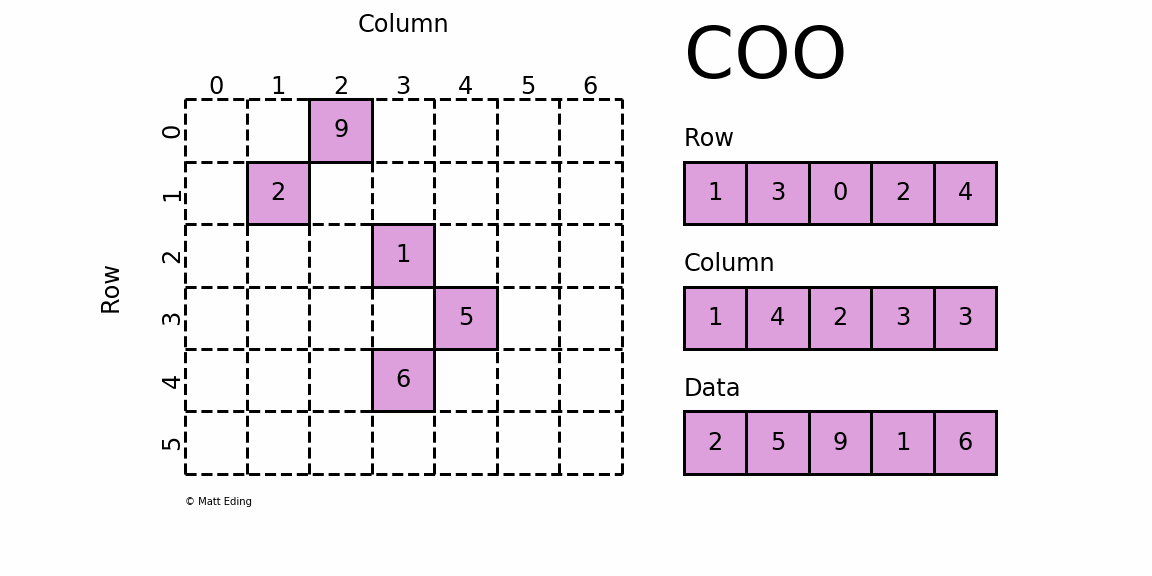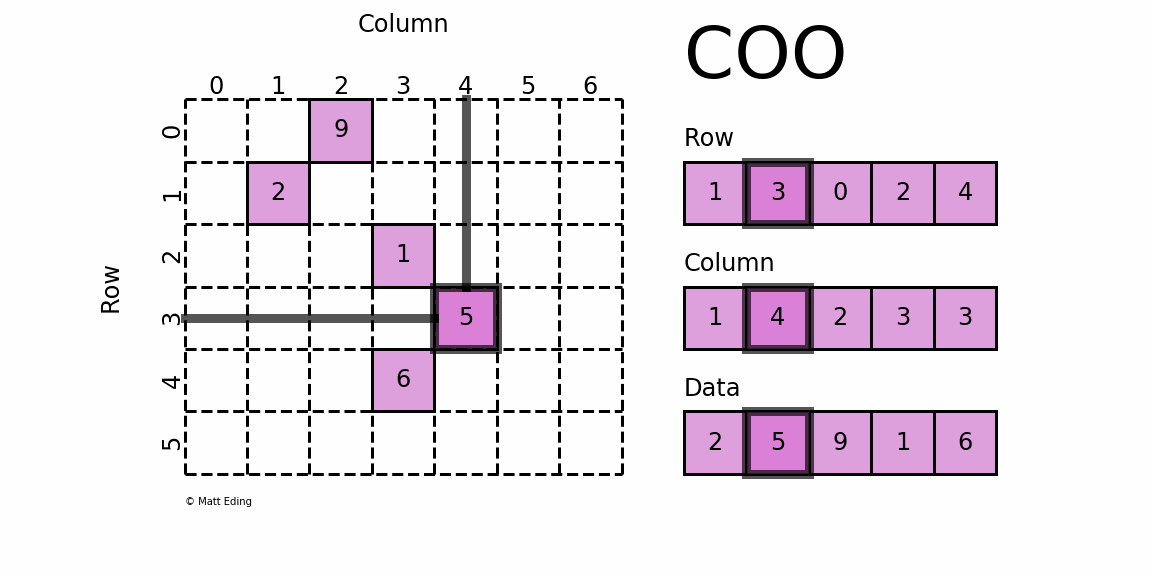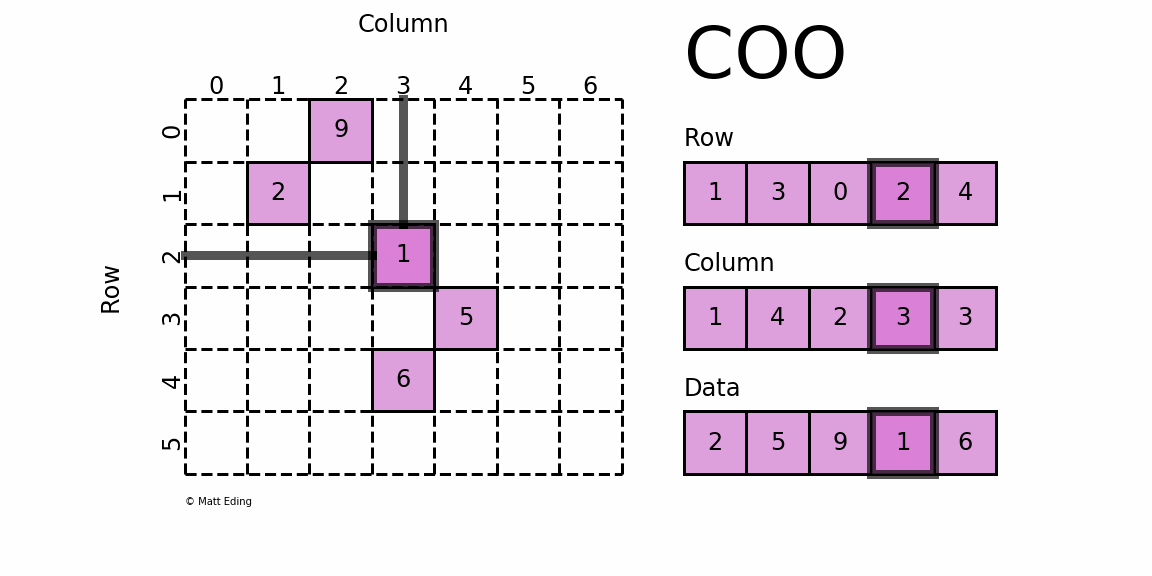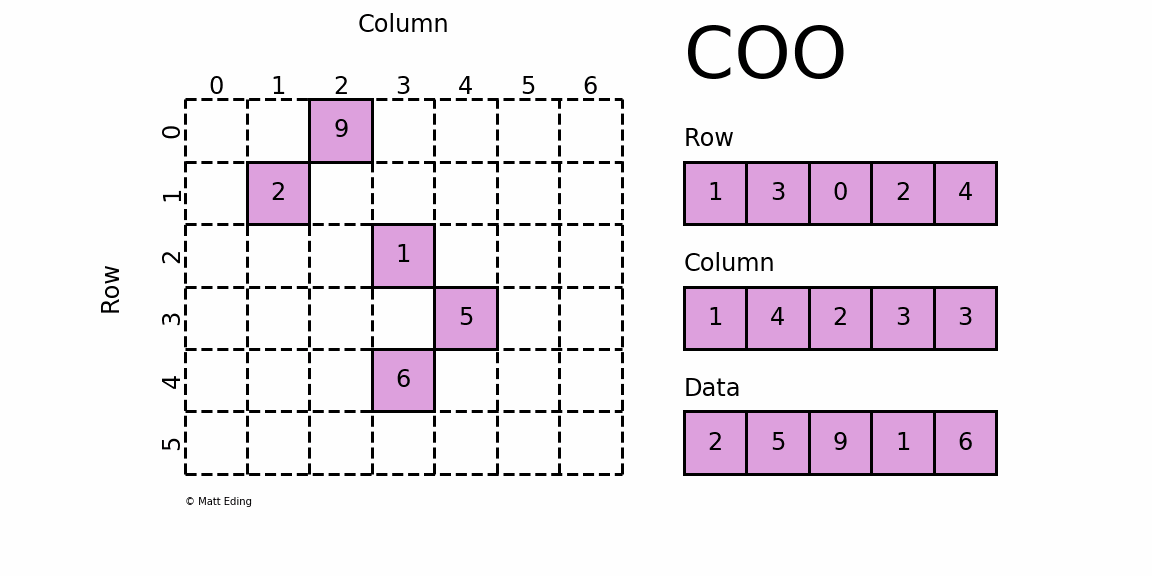
这种存储格式比较简单易懂,每一个元素需要用一个三元组来表示,分别是(行号,列号,数值),对应上图右边的一列。这种方式简单,但是记录单信息多(行列),每个三元组自己可以定位,因此空间不是最优的。
常用的开源矩阵求解库Eigen中的Triplet就对应这一操作。
(2) Compressed Sparse Row (CSR)/行优先
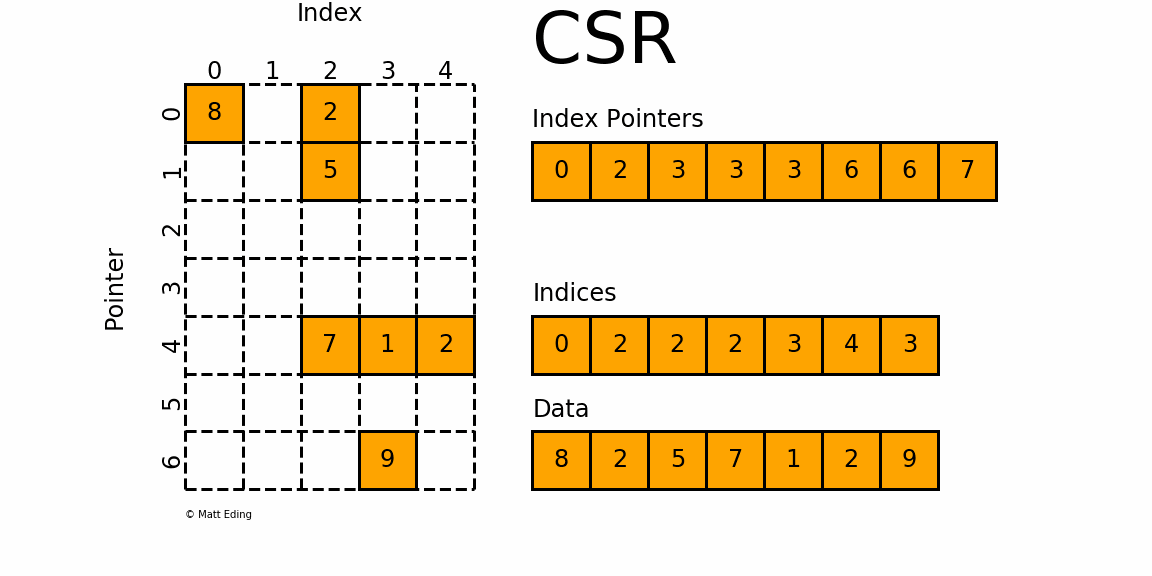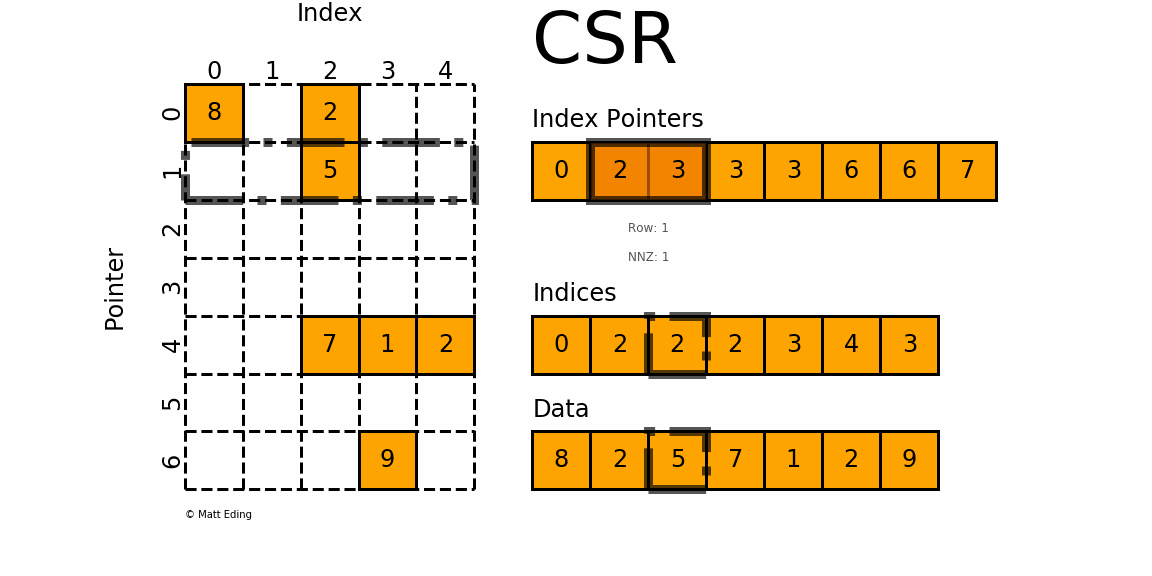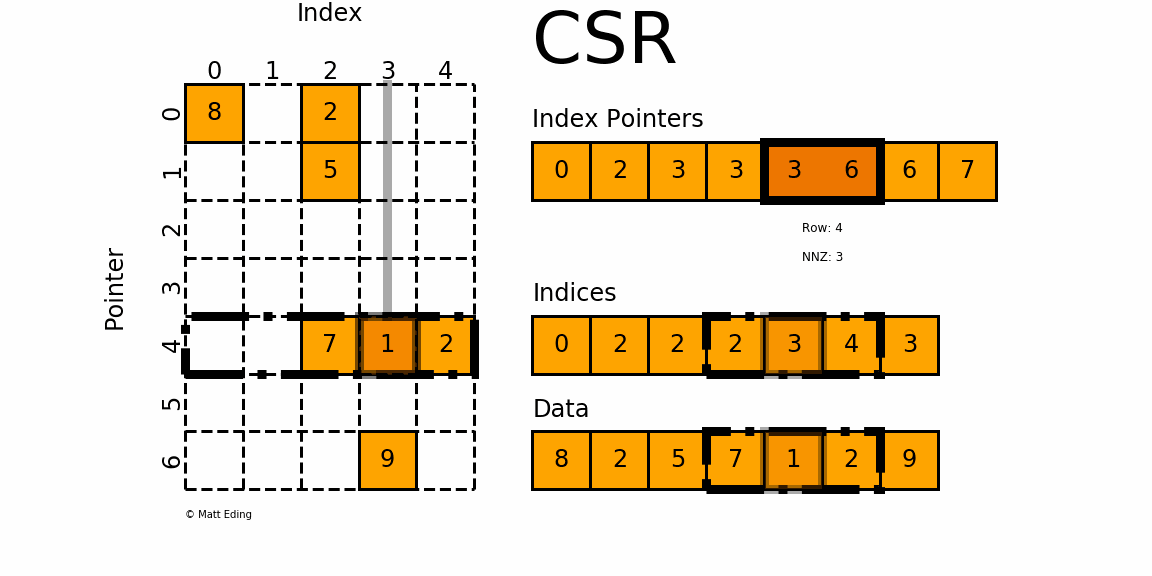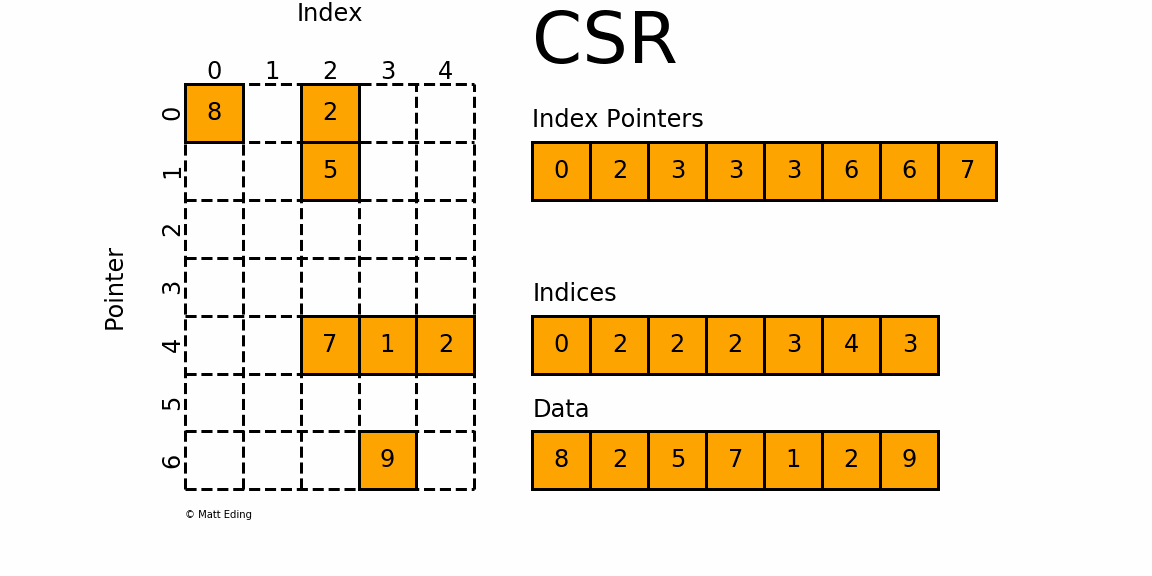
这是经常用的一种,我们会经常在一些标准的线性代数库或者数值运算库中看到此方式存储;CSR是比较标准的一种,也需要三类数据来表达:数值,列号,以及行偏移。CSR不是三元组,而是整体的编码方式。数值和列号与COO一致,表示一个元素以及其列号,行偏移表示某一行的第一个元素在values里面的起始偏移位置。
(3) Compressed Sparse Column (CSC)/列优先
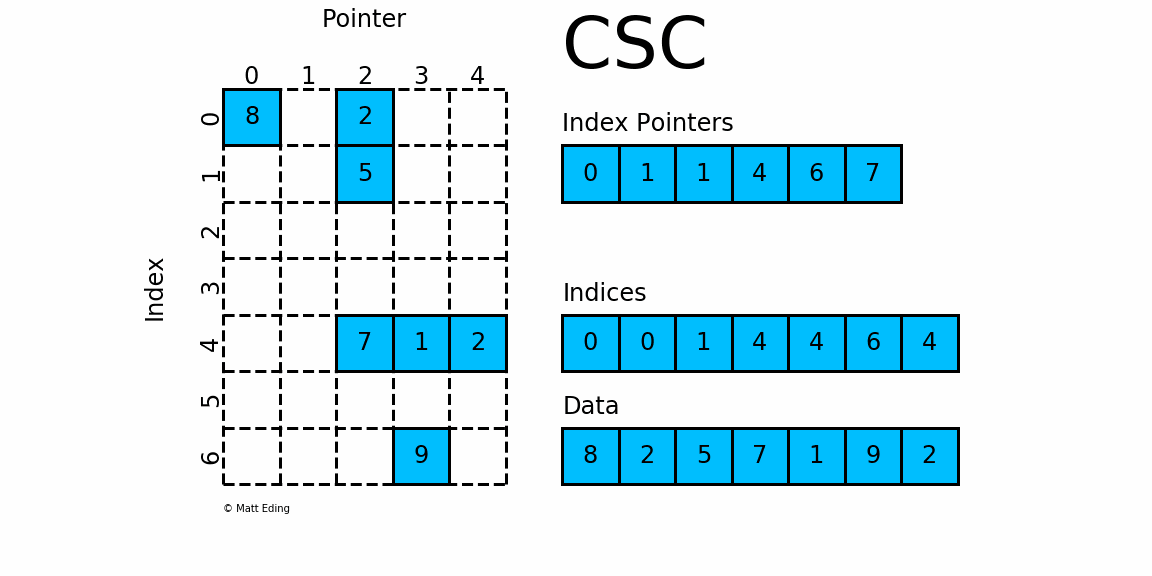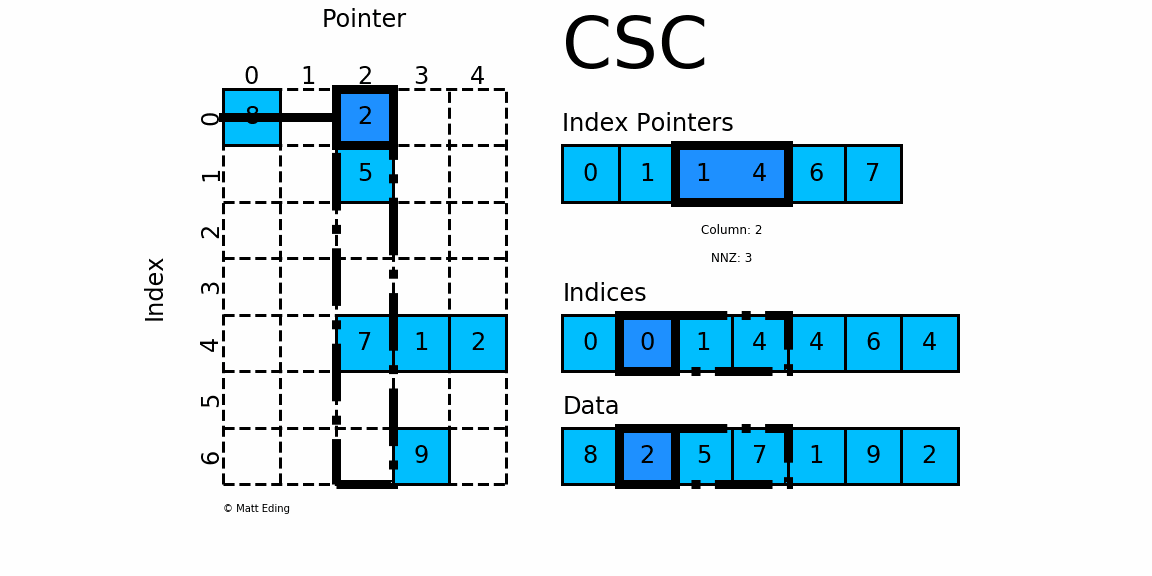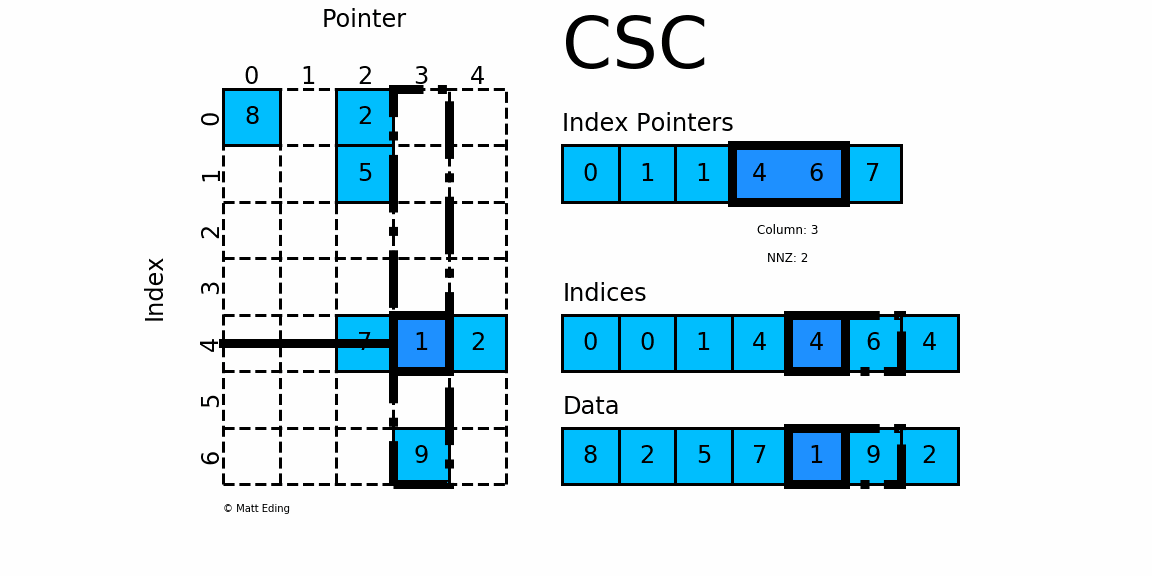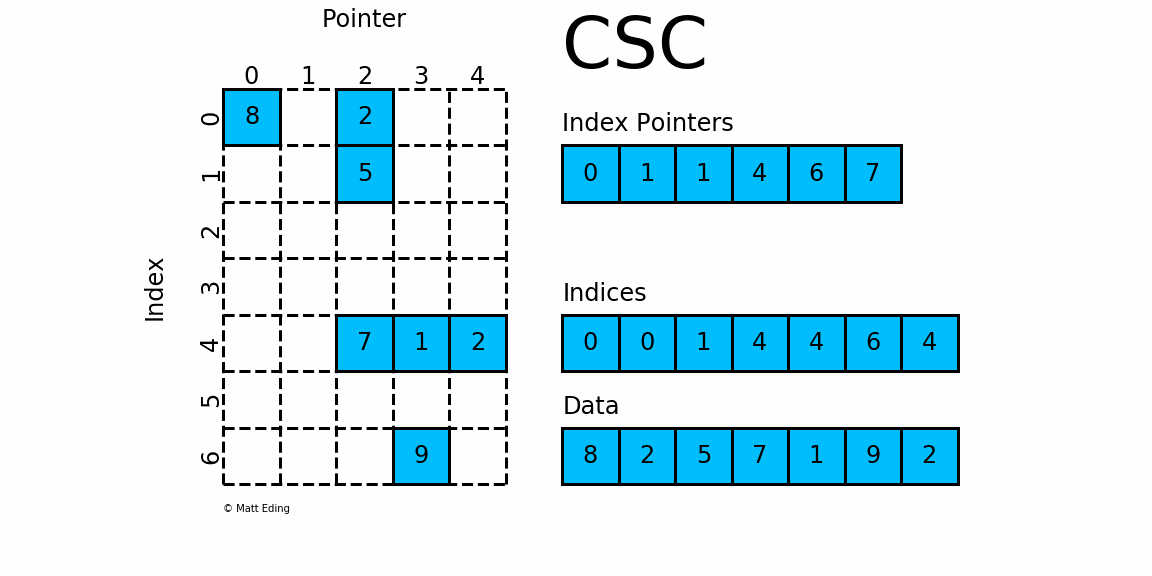
CSR是按行来存储一个稀疏矩阵的,其原理与CSC类似。indptr中的数据表示矩阵中每一行的数据在data中开始和结束的索引,而indices中的数据表示所对应的在data中的数据在矩阵中其所在行的所在列数。可以看出,在indptr、indices和data三个数组相同的情况下,通过CSC和CSR分别表示出来的矩阵互为转置关系。
注:上述图片来自Matt Eding的个人博客,更多矩阵压缩方法可参考Matt Eding’s Blog或CUDA手册。



